1.1.2. Решение квадратного уравнения в пространстве чисел.

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

Расширение поля комплексных чисел считается невозможным. Расширение поля комплексных чисел связывают с выявлением математической операцией над ними, которая не выполнялась бы в этом поле. В связи с отсутствием такой операции поле комплексных чисел определено как замкнутое. В этом заключена логическая ошибка. Ситуация, требующая расширения поля комплексных чисел существует и для этого необходимо вновь вернуться к рассмотрению решения квадратного уравнения. Рассмотрим классических ход решения квадратного уравнения

, где коэффициенты a, b действительные или комплексные.Произведем последовательно операции

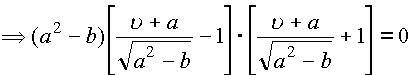Считаем . Произведение двух сомножителей XY равно нулю в трех случаях:

1) X=0,

3) .

(1.2.)

Третий случай определяет произведение делителей нуля. Первые два варианта дают классический случай решения и два корня квадратного уравнения в действительной и комплексной областях

Это тривиальное решение. Исключить из рассмотрения третий случай не оправдано с логической точки зрения. Два сомножителя не равные нулю, в произведении дающих ноль, существуют в пространстве комплексных чисел.

Обозначим

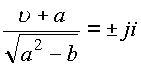
где было введено : .

Подставляя выражение в квадратное уравнение,

получим произведение

Откуда следует, что квадратное уравнение имеет еще два корня в пространственном поле чисел

Ввиду того, что отыскание корней не представляет трудностей. Появление коэффициента ji перед дескрименантом в решении квадратного уравнения определяет разветвление в решении в силу изменения размерности пространства. Квадратный корень имеет разветвление на отрицательное и положительное значение в любой размерности пространства и поэтому корни являются сопряженными. Поэтому квадратное уравнение имеет по меньшей мере четыре корня.

Пример: Имеем квадратное уравнение

Корни в действительной области чисел , уравнение разлагается на два сомножителя

для этого разложения действует два первых варианта равенства нулю произведения двух множителей.

Корни в комплексном пространстве чисел соответственно равны

, откуда , уравнение разлагается на два сомножителя

для этого варианта корней также действуют два первых варианта равенства нулю произведения двух множителей

Если во второе разложение подставить корни из плоскости –1 или 3 то разложение переходит в произведение делителей нуля (третий вариант равенства нулю произведений двух сомножителей )

где

Аналогичная ситуация получается при подстановке корней из пространства чисел в разложение в действительной области. Корни из пространства одного измерения лежат на изолированной оси пространства другого измерения.

Пример: Квадратное уравнение имеет четыре корня : в действительной области чисел,. В пространстве квадратное уравнение разлагается по двум равноценным вариантам

Подстановка любого корня уравнения из одной области пространства в разложения из другой области пространства дают произведение делителей нуля.

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com