 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
7.8 Расчет модели атома водорода.
В теоретической физике имеем ряд формул, вытекающих одна из другой и составленных из фундаментальных постоянных
Комптоновская длина волны электрона
см
Первый боровский радиус
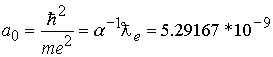см
Классический радиус электрона
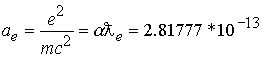см
Ионизационный потенциал водорода при бесконечной большой массе протона
эв
Постоянная тонкой структуры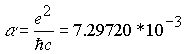 
Естественно все формулы связаны между собой, однако что лежит в основе этих формул до сих пор остается невыясненным. Покажем, что все эти формулы есть результат предельного соотношения. Имеем
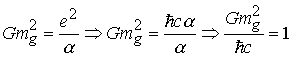и только поэтому одновременно соблюдается выражение для постоянной тонкой структуры
.
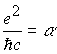Это выражение означает, что отношение гравитационного заряда фундаментальной массы к ее электрическому заряду равно обратной величине постоянной тонкой структуры
.
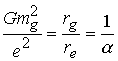Это предельное выражение реализуется на изолированном гравитационно-электромагнитном луче взаимодействующих полей.
Далее. Поделим правую и левую часть предельного соотношения на комптоновскую длину волны электрона
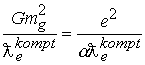получим 
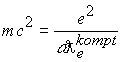, откуда имеем
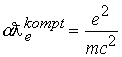т.е. получили классический радиус электрона 
.
Гравитационный заряд фундаментальных масс
на расстоянии комптоновской волны электрона 
превосходит электромагнитный заряд в 
. Этот вывод будет справедлив для всех микрочастиц заряженных и не заряженных ( протона, нейтрона и т.д.).
Рассмотрим с этих позиций, что было предложено в 1913 году Нильсом Бором.
Теория Нильса Бора считает, что движение электрона в атоме водорода происходит по круговой орбите радиуса
вокруг протона. Эта орбита определяется уравнением движения
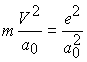и квантовым условием Бора 
, где V-скорость электрона, J-его момент количества движения, который предполагается равным 
.
Проведем последовательно преобразования уравнения движения, используя полученное предельное соотношение
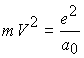. Заменим массу электрона на ее выражение через фундаментальную массу 
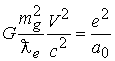, проведем сокращение при условии равенства 
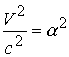. Имеем 
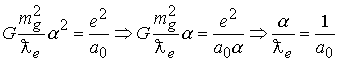. Откуда имеем выражение для первого боровского радиуса
.
Вывод. Взаимодействие двух фундаментальных масс
на расстоянии комптоновской волны электрона 
создает заряд е, определяет энергию электрона, который находится на первом боровском радиусе. Гравитационное взаимодействие фундаментальных масс на расстоянии боровского радиуса равно энергии взаимодействия двух зарядов на расстоянии комптоновской длины волны электрона.
Можно провести выкладки и в другой последовательности
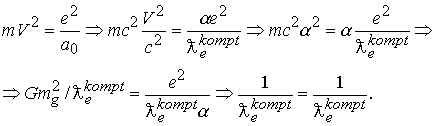
Если провести преобразования в обратном порядке при соблюдении соотношений
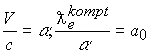, то предельное соотношение гравитационного луча даст уравнение динамического равновесия.
Если третье преобразование в этой цепочке поделить на 
1/2, то получим
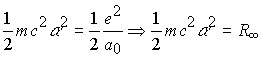
То есть получили энергию ионизации электрона в атоме водорода. Энергия основнового состояния атома водорода равна
.
Эту энергию можно выразить через фундаментальные постоянные
.
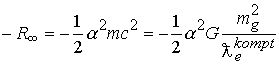
Предельное соотношение определяет гравитационно-электромагнитный луч. Из этого соотношения (как было показано) выводятся основные формулы структуры атома водорода и энергетические соотношения. Динамическое условие равновесия электрона на орбите является модификацией этого соотношения. Следствием этого является принадлежность орбит электрона пространству делителей нуля. В комплексном пространстве, в котором реализуются принципы интервала теории относительности орбита будет представлять комплекс вида
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com