 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
4.2. Критические линии при обтекании.
Из решения волнового уравнения следует, что комплексная скорость при обтекании тела конечных размеров в пространстве выразится
где
скорость распространения
возмущения в сплошной среде.
Скорость записана в простейшем виде без учета поворота в пространстве составляющих
Переходя к сферическим координатам, будем иметь
,
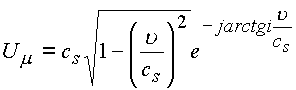так что модуль скорости равен
,
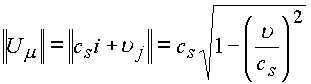а аргумент
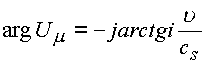
Исследуем возможные случаи при обтекании:
a)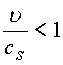 
; b) 
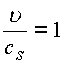; c)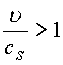 
;
В случае а) корень модуля будет действительной величиной, этот случай тривиален. В случае б) корень равен
, а аргумент arctg i. Движущееся тело
либо частица имеет общий e -туннель, со средой, в которой
происходит движение.
Суммарный вектор скорости указывает на точку,
лежащую на конусе-фильтре
делителей нуля. В случае с) корень
становится мнимым числом, и поэтому фактически
происходит поворот скорости по
углу f на величину p /2.
Этот случай показывает, что при увеличении скорости до величины, превосходящей скорость возмущения в среде, суммарный вектор скорости поворачивается на угол 90 град.
Вместе с этим происходит поворот части сплошной среды, так что в ней образуется двойная граница, воспринимаемая в аэродинамике, например как граница ударной волны.
С точки зрения (математики, этот эффект означает образование новой пространственной структуры и переход пространства в более высокую размерность и требуется переход в исследованиях к новому физическому аппарату и другим координатам
).Любая, дважды дифференцируемая функция, определенная в пространстве, удовлетворяет волновому уравнению. В то же время эта функция дает отображение не только потока, но и критических линий, поэтому конус может иметь любую конфигурацию в зависимости от формы тела и условий обтекания.
Если скорость переходит, условно говоря, через звуковой барьер, то критические точки растекаются на критические линии в пространстве.
При этом отображающая функция дает образы этих критических линий на поверхности летящего тела и эта поверхность списывается функцией
.
Критические точки в классическом решении определялись из условия
,
которое реализуется и в пространстве. В принципе это условие с точки зрения предлагаемого аппарата не несет структурного исследования изучаемого процесса. Поэтому в пространстве
к нему добавляется еще условие
, 
,
которое несет структурную нагрузку.
С этих позиций световой конус теория относительности
и конус "звукового барьера" являются явлениями одного класса. Они характеризуют критические переходы в структуре пространства. В этом смысл конуса-фильтра дискретных точек делителей нуля.Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com