 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
1.1.5. Геометрическая иллюстрация пространственного комплексного числа
Вершиной классической математики и математического анализа является теория функций комплексного переменного (ТФКП), основателем которой является французский математик О. Коши. Теория дошла до нашего времени почти в том виде, в котором она была создана.
Значительно усилив мощь математического аппарата в инженерных расчетах, теория Коши оставила инженерный аппарат плоским расчетным. Для перехода к описанию пространственных физических процессов и явлений требуется введение в аппарат дополнительных координат, которые не соответствуют определению пространственной точки и окрестности ее, которая заложена в теории Коши. В теоретической физике например, вводят матрицы, которые ближе к программному обеспечению чем к математическому аппарату.
Для описания пространственных явлений и процессов исследователи строят свои конкретные физико-математические модели. Инженерный расчет достигает успеха лишь в том случае, когда он проводится с соблюдением законов алгебры обычных чисел.
Сложность физических процессов, например, на уровне атомного ядра и электронных оболочек требует создание эффективной пространственной модели.
Теория Коши в этом плане дает предпосылки для построения такой пространственной модели и она используется в теоретической физике. Теоремы Коши об изолированных точках и вычетах, а также взаимосвязь точек на плоскости комплексных координат дают основание на пересмотр абстрактного понятия точки. Рассмотрим последовательно: линию, плоскость, пространство, опираясь на принятые понятия, но делая свои выводы.
Линия рассматривается как одномерное
пространство, как и делают современные
исследователи. Однако как только на линии
ставится точка ноль, как
начало координат, что означает на инженерном
языке привязку этой линии к реальному
пространству, назвать линию одномерным
пространством означает допустить грубейшую
ошибку. Переход по линии из ![]() через точку 0 к
через точку 0 к ![]() нельзя
не обогнув 0 по дужке и совершив оборот на угол
нельзя
не обогнув 0 по дужке и совершив оборот на угол ![]() .
.
![]()
Можно игнорировать этот факт,
называя линию одномерным пространством, но можно утверждать, что линия терпит разрыв в точке начале координат, какой бы минимальный радиусДужке
Далее рассматриваем установившееся понятие двумерного (плоского) пространства. Если плоскость рисуется без начала координат, то это понятие не несет физического смысла. Если плоскость привязана к реальному пространству, то в ней фиксируется начало координат. В этом случае логика предыдущих рассуждений вступает в силу. Окрестность нуля не принадлежит этому двумерному миру. Окрестность нуля выколотое двумерное пространство. Определение, ноль имеет неопределенный аргумент
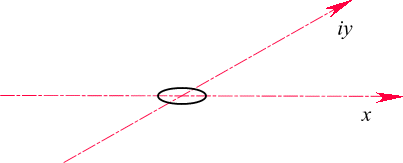
Нельзя пройти точку ноль по прямой, не обогнув ее по дужке в его окрестности. Можно радиус дужки устремить к нулю, однако физическая сторона и в этом случае не меняется. Определение нуля как
Продолжая эту логическую цепочку, восстановим к плоскости не линию,
как это делает классическая математика, а цилиндрическую трубочку радиуса окрестности нуля. Сфера в таком пространстве является сферой с проколотыми вершинами. Пространство внутри сферы между ее внутренней поверхность и наружной поверхностью цилиндрической оси есть пространство другого измерения, чем пространство вне сферы и внутри изолированной оси.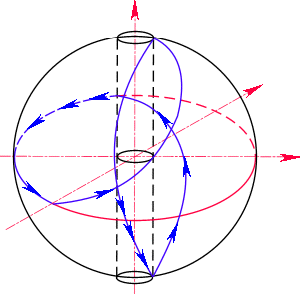
Простейшей пространственной кривой будет
кривая ![]() .Кривая
характеризуется двумя аргументами
.Кривая
характеризуется двумя аргументами ![]() и двумя радиусами : R-радиус
сферы ,
и двумя радиусами : R-радиус
сферы , ![]() -радиус
цилиндрической оси. Двигаясь по кривой
-радиус
цилиндрической оси. Двигаясь по кривой ![]() аргумент
аргумент ![]() получит
приращение
получит
приращение ![]() ,
аргумент
,
аргумент ![]() получит приращение
получит приращение ![]() .На кривую
.На кривую ![]() можно натянуть поверхность без
точек самопересечения и нельзя сжать без складок
в плоскую кривую. Более сложные кривые имеют,
выражаясь физическим языком, большее количество
намоток по поверхности сферы и цилиндрической
оси.
можно натянуть поверхность без
точек самопересечения и нельзя сжать без складок
в плоскую кривую. Более сложные кривые имеют,
выражаясь физическим языком, большее количество
намоток по поверхности сферы и цилиндрической
оси.
Становится очевидным почему при извлечении корня из+1 имели два разных корня
только при периодичности изменения аргументовПри такой геометрической интерпретации абстрактное понятие точки , линии , плоскости детализируются
: точка есть сфераИмеет
Комплексное пространство впервые введено в работах [1], [2], [3], [4]. Оно может быть интерпретировано как в цилиндрических, так и сферических координатах в соответствии с формулами, его определяющими.
Раскроем комплексы
z и s , входящие в формулу (1.3. и 1.4.).В комплексной плоскости имеем
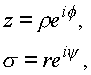
где r
, r - модули комплексных чисел z, s :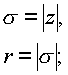
где
При таком обозначении комплексы
z, s определяются через свои полярные радиусы, соответственно равные: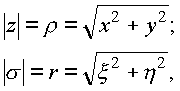
и аргументы f
= arg z, y = arg s , которые определены с точностью до любого слагаемого, кратного 2p :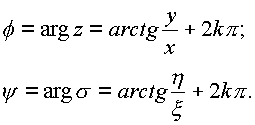
Следовательно, имеем
![]()
Так как единичные векторы
i и j (мнимые единицы) связаны в пространстве законом коммутативного умножения ij=ji, то комплекс может быть преобразован и к следующему виду:![]()
где соответственно имеем уже:
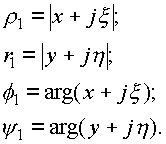
В дальнейшем будет показано, что в пространстве комплексных чисел нет выделенного направления и обе записи эквивалентны.
Далее, применяя к пространственному комплексу n формулу Эйлера, получим
![]()
где
R1 определен как комплексный модуль, равный![]()
![]() - комплексный аргумент, равный
- комплексный аргумент, равный
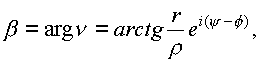
периодические свойства, которого будут выявлены в дальнейшем.
Преобразуем комплексный модуль по законам комплексной алгебры. Выделение действительного модуля дает выражение
![]()
а действительного аргумента
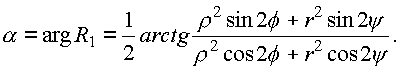
Таким образом, пространственный комплекс записывается в виде
(1.5.) |
где
R,Перейдем к геометрической иллюстрации комплексного пространства.
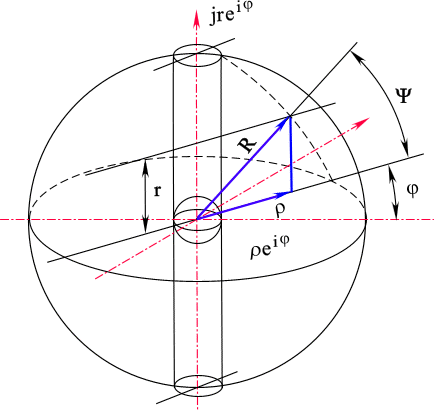
В цилиндрических координатах (рис. 4) в соответствии с формулой (1.3.) к плоскости
z=r eif восстановим из начала координат вектор js =jreiy , так что модуль r будет фиксировать расстояние от этой плоскости (z).При такой интерпретации вектор
js =jreiy при изменении![]()
- и аргумента y
![]()
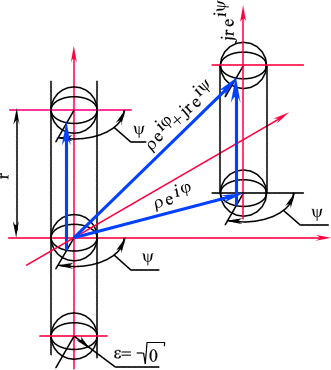
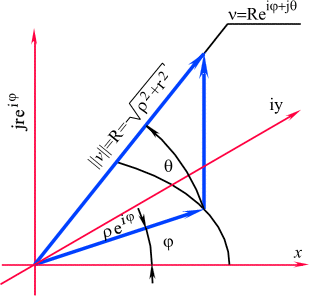
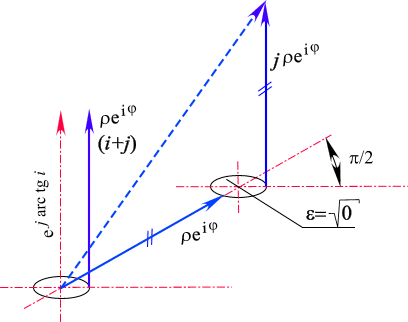
Рис. 5. Построение цилиндрической комплексной системы координат четырехмерного пространства. Сложение мнимых векторов в трехмерном пространстве Y.
опишет цилиндрическую ось, сечение которой будет иметь некоторый строго положительный радиус
e , e >0, в том числе и сколь угодно малый на любом сечении, параллельном плоскости (z). Таким образом, вектор js будет идти по образующей, фиксированной углом y на этой цилиндрической оси.Конкретная точка
n в цилиндрических координатах представляет сумму двух векторов: вектора r eif , лежащего в плоскости (z), и вектора jrejy , лежащего на цилиндрической оси.В простейшем случае построенное четырехмерное пространство переходит в трехмерное. Это происходит при равенстве аргументов в плоских комплексах
z, s .В этом случае все параметры, определяющие точку n , становятся действительными
![]()
где
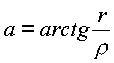 - теперь тоже действительное число.
- теперь тоже действительное число.
Изображение такой точки представлено на рис. 5, где угол
a обозначен через q . В этом случае точка определена тремя независимыми переменными r, r , f ;![]()
Образующая, по которой идет вектор
jreif , фиксирована углом f , равным углу комплекса, лежащего в плоскости (z). Все три вектора лежат в одной плоскости: два составляющих z=r eif , s =jreif и суммарный вектор n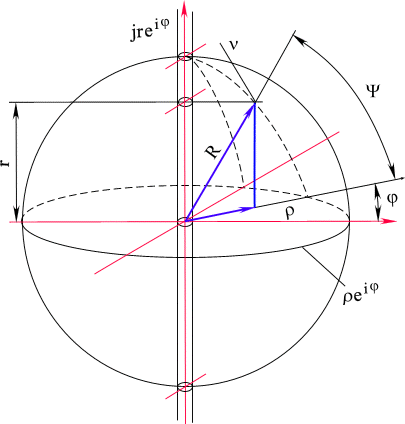
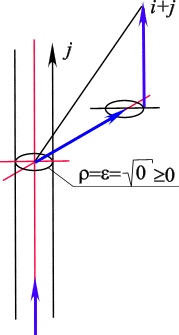
При постоянном модуле
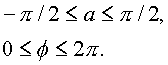
суммарный вектор
n опишет сферу с выколотыми вершинами по оси js (рис. 6, рис. 7.а.). Точка n в пространстве (n ) фиксирована тремя действительными параметрами R, f , a.Формула (1.5.) определяет сферические пространственные комплексные координаты:
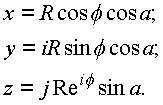
Третья координата имеет вращение вокруг оси.(Этот вариант не рассматривается в квантовой механике , а вводится другими условиями , чтобы результат соответствовал эксперименту).
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com