В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО [Оглавление]
	Елисеев В.И. Числовое поле. Введение в ТФКПП. Елисеев В.И. Оси координат физической реальности. Елисеев В.И. Введение в ТФКПП. 2003 Елисеев В.И. Числовое поле. Введение в ТФКПП. 2006 Елисеев В.И. Оси координат физической реальности. 2012

---

1.1.8. Замкнутость пространственной комплексной алгебры

Докажем, что построенная алгебра с коммутативным умножением является замкнутой и элементы в ней определены однозначным образом независимо от способа их преобразования.

Ввиду коммутативности умножения единичных векторов i, j

ij=ji

комплекс n запишем в двух видах:

	(1.19.)
	(1.20.)

Согласно комплексной интерпретации пространственного числа по формуле (1.19.) геометрическая интерпретация соответствует цилиндрическим и сферическим координатам с выколотой осью, перпендикулярной плоскости (z), а по формуле (1.20.) выколотая ось перпендикулярна плоскости (i, j). Для наглядности первую ось можно рассматривать как лежащую в плоскости чертежа (рис. 13.), а вторую перпендикулярно плоскости чертежа.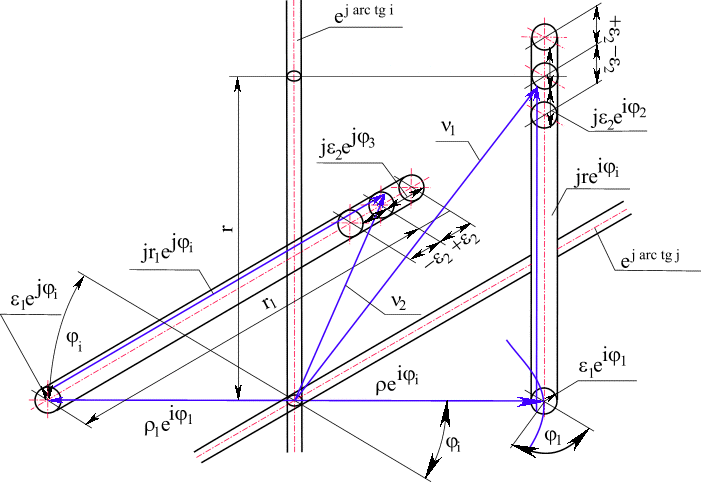

Рис. 13. Изолированные направления в многомерном комплексном пространстве.

Первая ось имеет изолированное направление , вторая - изолированное направление .

В сферических координатах согласно формуле (1.6.) комплексы (1.19.), (1.20.) запишутся в виде:

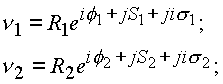
Докажем, что точка в комплексном пространстве определяется единственным образом и ее расположение не зависит от ориентации изолированных осей в пространстве. Преобразования комплексов (1.19.), (1.20.) инвариантны относительно выбранных изолированных направлений. Для этого следует доказать, что

R₁=R₂, f ₁=f ₂, S₁=S₂, s ₁=s _2.

Доказательство. Произведем вычисление модулей комплексов (1.19.), (1.20.):

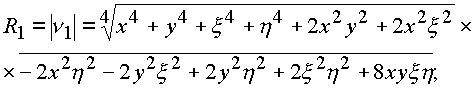
Раскрывая модуль последнего выражения, получим:

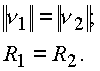
Угол f ₁ определяется аргументом выражения первого комплексного модуля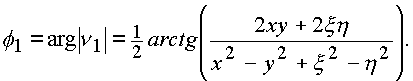

Углы S₁ и s ₁, выделяются, когда комплекс n ₁ представлен в виде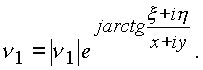

Аргумент комплекса выразим через логарифмическую функцию

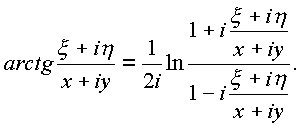
Действительная часть логарифма даст угол S₁, а мнимая угол s ₁. Соответственны имеем: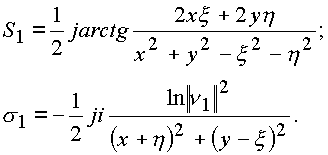

Применяя последовательно тот же расчетный алгоритм к комплексу (1.20.), получим требуемые для доказательства равенства.

Например, угол S₂ определяется как аргумент комплекса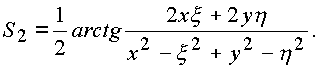

Видно, что он равен углу S₁, S₂=S₁ и так далее.

Расчет показывает, что при любом представлении пространственного комплекса n точка в пространстве определяется единственным образом.

Все операции в комплексном пространстве инвариантны относительно расположения выколотых изолированных осей.

Например. Комплекс n =ij=ji определяет единственную точку, которая лежит на сфере радиуса и фиксирована углами S =p /2, f =p /2, s =0.

[Следующий параграф]

---

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11] 

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com