 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
1.6. Вычеты в пространстве. Вычисление интегралов с помощью вычетов.
В пространстве имеет место две формулы вычетов:криволинейный и поверхностный. Введем определение вычетов.
Пространственным криволинейным вычетом
функции ![]() в точке
в точке ![]() называется коэффициент
называется коэффициент ![]() ряда Лорана для функции в
окрестности точки
ряда Лорана для функции в
окрестности точки ![]() , то есть
число, которое обозначается символом
, то есть
число, которое обозначается символом ![]()
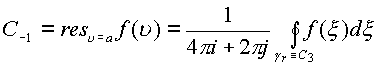 |
(1.61.) |
Формула следует из формулы для определения
коэффициентов ряда Лорана. Под кривой ![]() понимаем кривую типа
понимаем кривую типа ![]() , которая натянута на
сферу радиуса
, которая натянута на
сферу радиуса
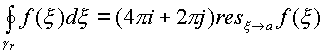 |
(1.62.) |
Очевидно, что если точка
a точка регулярности функции, либо устранимая особая точка, то вычет равен нулю. Если в разложении функции в ряд Лорана отсутствует с первой отрицательной степенью n=-1, то вычет равен 0.Поверхностным вычетом функции ![]() в точке
в точке
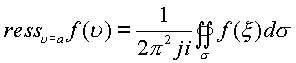 , , |
(1.63.) |
где ![]() -
поверхность, натянутая на кривую
-
поверхность, натянутая на кривую ![]() без точек самопересечения,
радиус которой равен
без точек самопересечения,
радиус которой равен ![]() . Из
формул для коэффициентов ряда
. Из
формул для коэффициентов ряда
Лорана получим ![]() .
Следовательно двойной интеграл равен
.
Следовательно двойной интеграл равен
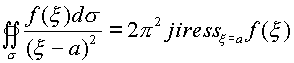 |
(1.64.) |
Вычисление вычета в полюсе простого или
кратного определяется видом ряда Лорана для
функции. Если имеем 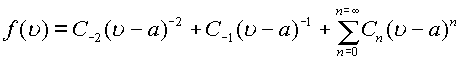 , откуда
находим
, откуда
находим
![]() , так что
, так что ![]() , а также
, а также ![]() , так
что
, так
что ![]() .
.
Если ряд Лорана имеет вид
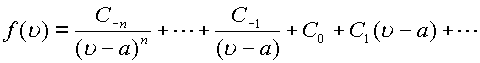 то функция в
окрестности точки
то функция в
окрестности точки ![]() имеет полюс
кратности n. Умножая это разложение на
имеет полюс
кратности n. Умножая это разложение на ![]() , дифференцируя n-1 раз и затем
переходя к пределу при
, дифференцируя n-1 раз и затем
переходя к пределу при ![]() получим
выражение
получим
выражение
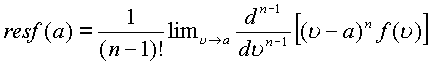 |
(1.65.) |
По той же схеме получим
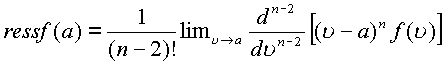 |
(1.66.) |
Пример. Определить вычет функции ![]() в точке
в точке ![]() . Функция разлагается в ряд Лорана в
окрестности точки
. Функция разлагается в ряд Лорана в
окрестности точки ![]() в виде
в виде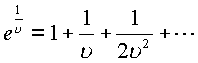 , где
, где 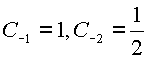
Следовательно 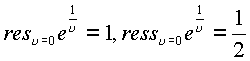 . Откуда имеем
. Откуда имеем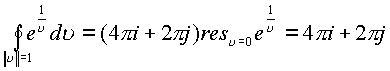
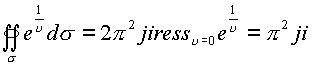 .
.
Пример. Пусть 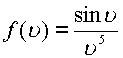 . Разложение
функции
. Разложение
функции ![]() в ряд Тейлора дает
представление функции
в ряд Тейлора дает
представление функции ![]() в виде
в виде 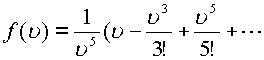
Откуда 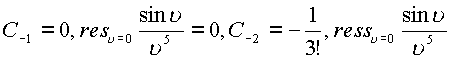 . Двойной интеграл
. Двойной интеграл
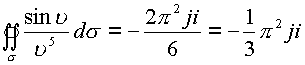
Пример. Пусть 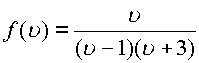 .
Функция имеет полюс первого порядка в точке
.
Функция имеет полюс первого порядка в точке![]() и полюс первого порядка в точке
и полюс первого порядка в точке ![]() .Поэтому по формуле
имеем
.Поэтому по формуле
имеем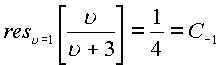
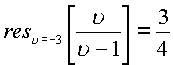 . Данная функция в пространстве
имеет еще две особые точки, которые
соответствуют корням алгебраического уравнения
стоящего в знаменателе. Последовательно получим
. Данная функция в пространстве
имеет еще две особые точки, которые
соответствуют корням алгебраического уравнения
стоящего в знаменателе. Последовательно получим 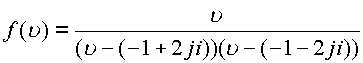 Особые изолированные
пространственные точки позволят вычислить еще
два вычета
Особые изолированные
пространственные точки позволят вычислить еще
два вычета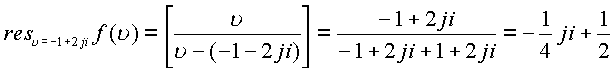
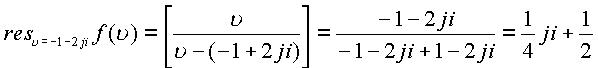 .
.
Пример. Рассмотрим функцию 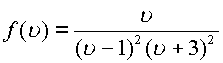 .
Функция имеет особые точки
.
Функция имеет особые точки ![]() полюс
второго порядка,
полюс
второго порядка, ![]() , полюс
второго порядка. Используя формулу для расчета
вычетов кратных полюсов будем последовательно
иметь.
, полюс
второго порядка. Используя формулу для расчета
вычетов кратных полюсов будем последовательно
иметь.
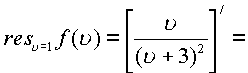
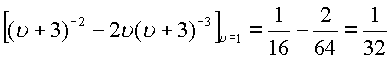
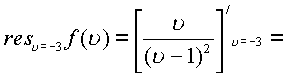
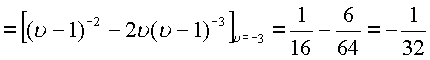
Функция имеет также два пространственных полюса второго порядка (см. пример )
![]()
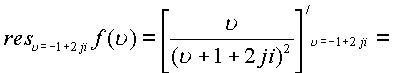
![]()
![]()
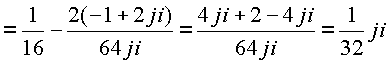
![]()
![]()
![]()
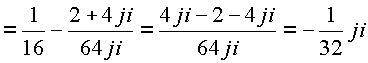 .
.
По формуле вычислим пространственные вычеты
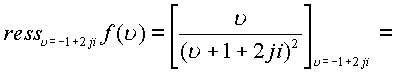
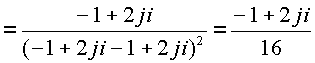
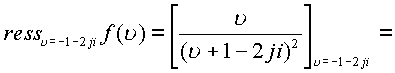
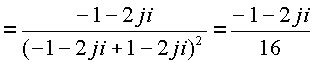
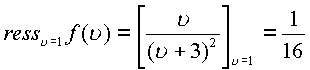
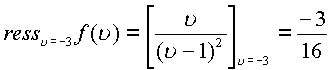
Пример. Пусть дана функция 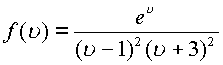 .
Используя результаты предыдущего примера,
вычислим пространственные вычеты.
.
Используя результаты предыдущего примера,
вычислим пространственные вычеты.
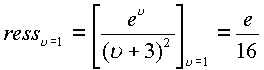
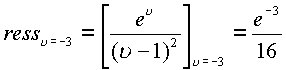
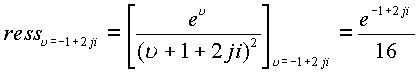
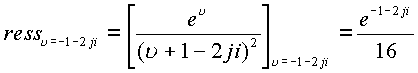
Пример . Пусть дана функция 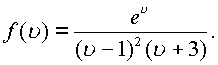 Определить
пространственные вычеты. Представим функцию в
следующем виде
Определить
пространственные вычеты. Представим функцию в
следующем виде 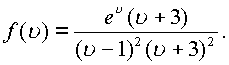 Используя
результаты предыдущего примера будем иметь
Используя
результаты предыдущего примера будем иметь
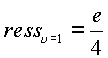
В пространстве ![]() функция
представима также в виде
функция
представима также в виде 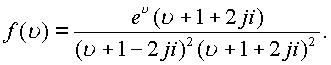
Откуда будем иметь 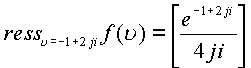
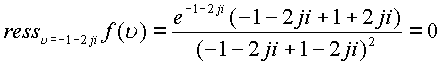 . Эти
выкладки показывают, что пространственный
корень
. Эти
выкладки показывают, что пространственный
корень ![]() является особой точкой
первого порядка.
является особой точкой
первого порядка.
Вычет в бесконечно удаленной точке.
В соответствии с комплексной пространственной
алгебре элемент ![]() изображается
в сферических координатах в виде
изображается
в сферических координатах в виде ![]() , так что бесконечная точка
характеризуется бесконечным радиусом модулем
, так что бесконечная точка
характеризуется бесконечным радиусом модулем ![]() Точка ноль
определяется в пространстве как это
неоднократно утверждалось в виде
Точка ноль
определяется в пространстве как это
неоднократно утверждалось в виде ![]() и произведением
и произведением ![]() , где параметры
, где параметры ![]() действительные, а
действительные, а ![]() .
.
Если положить 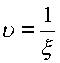 и
рассматривать функции
и
рассматривать функции 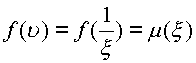 , тогда
функция
, тогда
функция ![]() будет аналитической в
некоторой окрестности точки ноль, которая будет
особой точкой того же типа, что и точка
будет аналитической в
некоторой окрестности точки ноль, которая будет
особой точкой того же типа, что и точка ![]() для функции
для функции ![]()
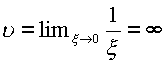 или на
изолированной оси
или на
изолированной оси 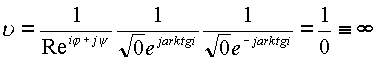
Теорема. Пусть функция ![]() непрерывна
на границе области G поверхности
непрерывна
на границе области G поверхности ![]() , натянутой без
точек самопересечения на пространственную
кривую типа
, натянутой без
точек самопересечения на пространственную
кривую типа ![]() и
аналитична внутри этой области всюду, кроме
конечного числа особых точек
и
аналитична внутри этой области всюду, кроме
конечного числа особых точек ![]() ,
тогда имеем в пространстве Y следующие
соотношения
,
тогда имеем в пространстве Y следующие
соотношения
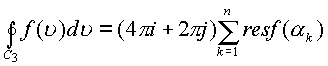
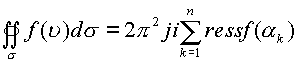
Если точка ![]() лежит внутри
области G и если точка
лежит внутри
области G и если точка ![]() также
принадлежит этой области, то
также
принадлежит этой области, то
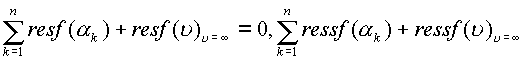
Если внутри области G имеется контур Г или
поверхность ![]() содержащими
внутри себя особые точки
содержащими
внутри себя особые точки ![]() , то
справедливы следующие интегральные соотношения
, то
справедливы следующие интегральные соотношения
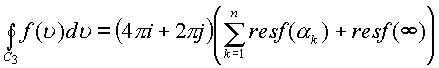
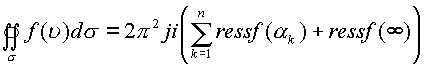
Вычетом функции в бесконечной точке будет
число 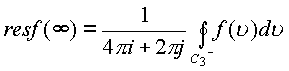 , а также
, а также
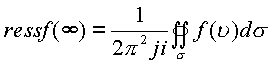 , где
поверхность
, где
поверхность ![]() натянута
на кривую
натянута
на кривую ![]() достаточно большой
сферы
достаточно большой
сферы ![]() , которая проходится в
обратном направлении. Поэтому вычеты равны
, которая проходится в
обратном направлении. Поэтому вычеты равны
![]() , где
, где ![]() есть коэффициенты перед
есть коэффициенты перед ![]() соответственно в лорановском
разложении функции в окрестности бесконечно
удаленной точке.
соответственно в лорановском
разложении функции в окрестности бесконечно
удаленной точке.
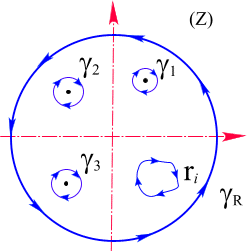
Рис. 30. Связность области в комплексной плоскости.
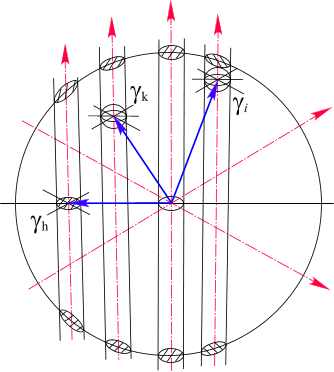
Рис. 31. Связность области в комплексном пространстве.
В комплексной плоскости Z теорема о вычетах
соответствовала Рис. 30, где область G находится
между границей![]() ,
где
,
где ![]() и Г, состоящей
из конечного числа ограниченных кусочно гладких
кривых
и Г, состоящей
из конечного числа ограниченных кусочно гладких
кривых ![]() , где
, где ![]()
В комплексном пространстве Y рассматривается
сфера с поверхностью, натянутой на бесконечно
большой радиус ![]() .
Особые точки окружены сферами бесконечно малого
радиуса
.
Особые точки окружены сферами бесконечно малого
радиуса ![]() . Так как через особую
точку проходит изолированное направление, то на
границе области фиксируются проколы поверхности
бесконечно малого радиуса. (Рис. 31.)
. Так как через особую
точку проходит изолированное направление, то на
границе области фиксируются проколы поверхности
бесконечно малого радиуса. (Рис. 31.)
Пример. Вычислить интеграл 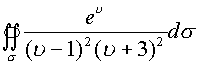 , где поверхность
, где поверхность ![]() натянута на сферу
натянута на сферу ![]() .
В области
.
В области ![]() функция имеет
четыре особые пространственные точки
функция имеет
четыре особые пространственные точки
![]() . Вычеты во
всех особых точках рассчитаны в примере , поэтому
в соответствии с теоремой о вычетах имеем
. Вычеты во
всех особых точках рассчитаны в примере , поэтому
в соответствии с теоремой о вычетах имеем
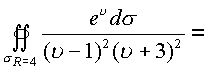
![]()
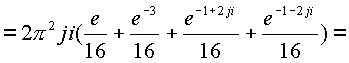
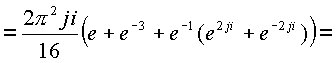
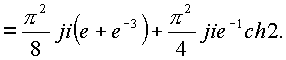
Пример . Вычислить интеграл по поверхности
натянутой на ![]()
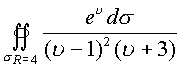 .
Пространственные вычеты согласно примера для
данной функции равны
.
Пространственные вычеты согласно примера для
данной функции равны 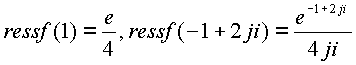 . В
соответствии с теоремой о вычетах будем иметь
. В
соответствии с теоремой о вычетах будем иметь 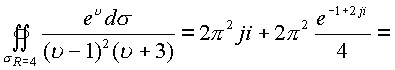
В дальнейшем можно произвести выделение первой и второй комплексной части
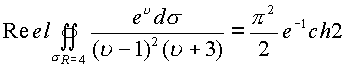
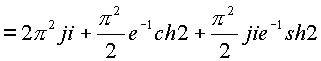
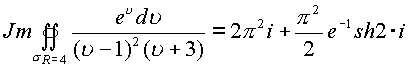
Интегралы вида 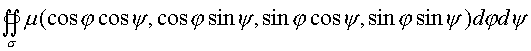 , где
поверхность
, где
поверхность ![]() натянута
на сферу радиуса
натянута
на сферу радиуса ![]() , так что
переменные
, так что
переменные ![]() изменяются
соответственно в пределах
изменяются
соответственно в пределах 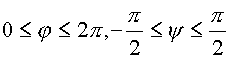 .
Для сокращения записей введем обозначения
.
Для сокращения записей введем обозначения ![]() . Так, что интеграл перейдет в
интеграл
. Так, что интеграл перейдет в
интеграл 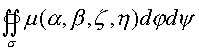
На поверхности сферы имеем ![]() и
введенные переменные могут быть записаны через
одну переменную
и
введенные переменные могут быть записаны через
одну переменную ![]() в комплексном
виде
в комплексном
виде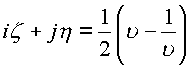
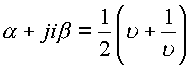 . Элемент площади
. Элемент площади ![]() , откуда
получаем
, откуда
получаем ![]() и в силу
и в силу ![]() будем иметь
будем иметь 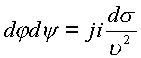 .
Исходный интеграл сводится к вычислению
двойного интеграла по поверхности
.
Исходный интеграл сводится к вычислению
двойного интеграла по поверхности 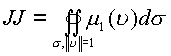 , где
, где 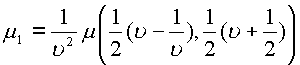 -есть
рациональная функция от
-есть
рациональная функция от ![]() .
Тогда по теореме о вычетах
.
Тогда по теореме о вычетах
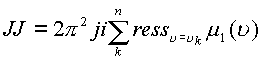 , где
, где ![]() - все полюсы
рациональной функции
- все полюсы
рациональной функции ![]() ,
лежащие в сфере
,
лежащие в сфере ![]() .
.
Пример . Вычислить интеграл 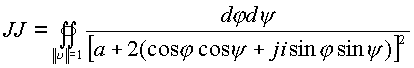
Преобразуем знаменатель. 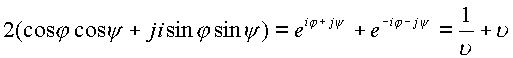
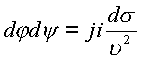 . Подставляя полученные
выражения в исходный интеграл, будем иметь
. Подставляя полученные
выражения в исходный интеграл, будем иметь
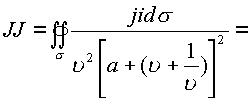
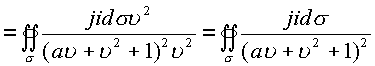
Знаменатель имеет корни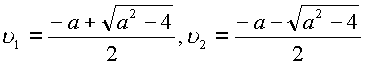 .
Первый корень при
.
Первый корень при ![]() является
особой точкой подынтегральной функции –полюсом
второго порядка.
является
особой точкой подынтегральной функции –полюсом
второго порядка.
Знаменатель имеет два пространственных корня 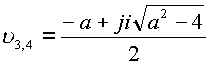 . Пространственные корни при
. Пространственные корни при ![]() имеют модуль
имеют модуль ![]() и не являются особыми точками
подъинтегральной функцией. Если принять
и не являются особыми точками
подъинтегральной функцией. Если принять ![]() , то
, то 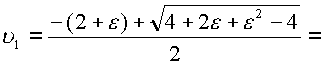
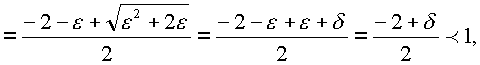 где
где ![]() . При тех же условиях
. При тех же условиях
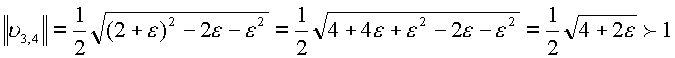 .
.
Поэтому согласно теореме о вычетах имеем 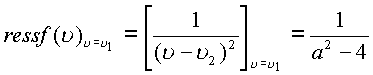 . Окончательно интеграл равен
. Окончательно интеграл равен
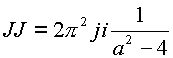
Подынтегральную функцию преобразуем на сумму
первых комплексных функций. Для этого обозначим ![]() и подставим в подынтегральную
функцию
и подставим в подынтегральную
функцию
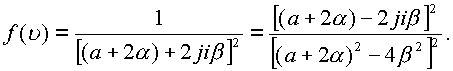 Следовательно
первая комплексная часть равна
Следовательно
первая комплексная часть равна 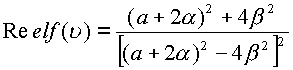 , вторая комплексная часть равна
, вторая комплексная часть равна
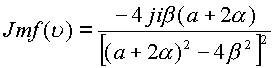 , В
результате имеем расчет двух двойных интегралов
, В
результате имеем расчет двух двойных интегралов
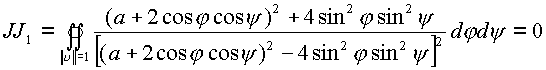
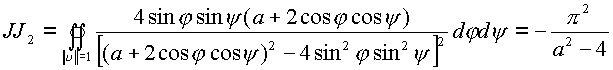
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com