 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
1.3.2. Интеграл и первообразная.
Определение интеграла вдоль кривой С в комплексном пространстве по виду ничем не отличается от определения интеграла в действительной и комплексной областях.
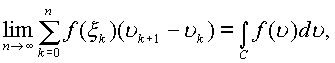
где
![]() При
доказательстве существования интеграла в
комплексной плоскости Z предел
сводили к двум интегралам от действительных
функций. В пространстве предел достаточно свести
к интегралам от комплексных функций. В самом деле
При
доказательстве существования интеграла в
комплексной плоскости Z предел
сводили к двум интегралам от действительных
функций. В пространстве предел достаточно свести
к интегралам от комплексных функций. В самом деле
![]()
![]() ,
,![]()
![]() . Обозначим
также
. Обозначим
также ![]() ,
, ![]() .
Подставляя в интегральную сумму получим
.
Подставляя в интегральную сумму получим
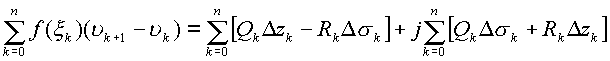
Переходя к пределам получим
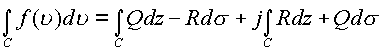
Существование интеграла в комплексном пространстве сводится к существованию двух комплексных интегралов
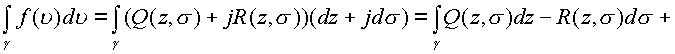
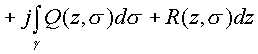
Функции
![]()
![]()
![]()
![]()
а также имеем
![]() .
Подставляя в интеграл и отделяя все интегралы с
мнимыми коэффициентами получим
.
Подставляя в интеграл и отделяя все интегралы с
мнимыми коэффициентами получим
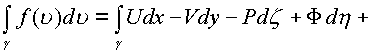
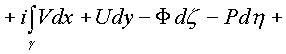
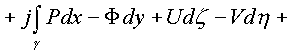
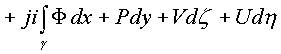 .
.
Существование криволинейного интеграла свелось к существованию и определению криволинейных интегралов от функций четырех действительных переменных. Для исследования этих интегралов необходимо обратиться к теоремам Стокса, Грина, Остроградского.
Рассмотрим формулу Грина. Пусть функции от двух действительных переменных
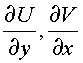 непрерывны в простой области G. Тогда справедливо равенство
непрерывны в простой области G. Тогда справедливо равенство
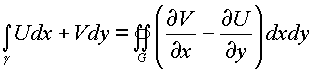 , где
криволинейный интеграл берется по границе
, где
криволинейный интеграл берется по границе ![]() области G в
положительном направлении., так что формула
Грина связывает интеграл по границе области с
интегралом по самой области. Важнейшим
условием в определении интеграла является
свойство области G. Введено
определение. Область G на
плоскости называется односвязной, если для
любого замкнутого контура, лежащего в этой
области, ограниченная им часть плоскости целиком
принадлежат области G. Для
таких областей независимость криволинейного
интеграла от пути интегрирования определяется
следующими условиями :
области G в
положительном направлении., так что формула
Грина связывает интеграл по границе области с
интегралом по самой области. Важнейшим
условием в определении интеграла является
свойство области G. Введено
определение. Область G на
плоскости называется односвязной, если для
любого замкнутого контура, лежащего в этой
области, ограниченная им часть плоскости целиком
принадлежат области G. Для
таких областей независимость криволинейного
интеграла от пути интегрирования определяется
следующими условиями :
1.Для любого замкнутого контура
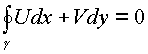 .
.
2. Для любых двух точек А,В в
области G криволинейный интеграл 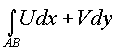 не зависит от
кривых
не зависит от
кривых ![]() ,расположенных
в этой области.
,расположенных
в этой области.
3. Выражение ![]() является полным дифференциалом
функции F(x,y), существующей в
области G, такой, что
является полным дифференциалом
функции F(x,y), существующей в
области G, такой, что![]() . При этом для
любой кривой
. При этом для
любой кривой ![]() из области G имеет
место равенство
из области G имеет
место равенство
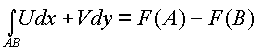
Все три условия эквивалентны равенству
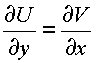 , выполняемому в
области G.
, выполняемому в
области G.
В пространстве трех действительных переменных имеет место формула Стокса, сформулированная следующим теоремой
:Пусть гладкая
xyz проектируемая ориентируемая поверхность Ф ограничена кусочно-гладким контуромИмеют непрерывные частные производные первого порядка. Тогда справедлива формула
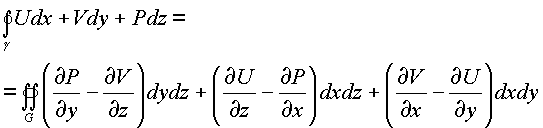 ,
,
где контур
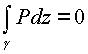 получается формула Грина.
В пространстве x,y,z вводится
понятие поверхностно односвязной области G, такой, что
получается формула Грина.
В пространстве x,y,z вводится
понятие поверхностно односвязной области G, такой, что
для любого контура
Независимость криволинейного интеграла от пути интегрирования доставляется также тремя условиями
:1) если выполняется равенство
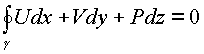 ;
;
2) если выполняется условие
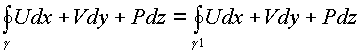 ;
;
3) если выражение Udx+Vdy+Pdz является полным дифференциалом некоторой функции F(x,y,z), определенной в области G
![]() , так что
, так что
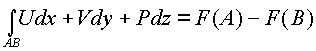
Все три условия заменяются тремя равенствами
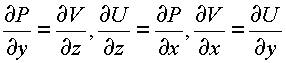
Поверхность Ф в формуле Грина расположена на одной проекционной площадке. Сочетание двух независимых переменных (
X,Y) дают одну проекционную площадку.Поверхность Ф в формуле Стокса имеет три проекционные площадки. Сочетание из трех по два рано трем.
Пространственный комплексный интеграл сначала свели к двум комплексным интегралам, каждый из которых определен на комплексной плоскости
имеют частные производные
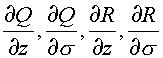 .
.
В комплексном пространстве можно определить область
G, ограниченную кривой С с соблюдением всех условий теоремы и формулы Грина. Применяя формулу Грина к криволинейному интегралу, выраженному в пространственных комплексах (z,Два интеграла
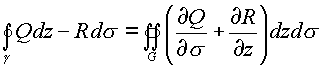
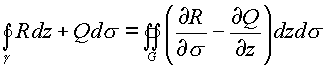
Как следствие получаем условие независимости криволинейного интеграла в пространстве в комплексном виде
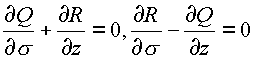
Эти условия были исследованы при исследовании комплексного аргумента. Раскрывая частные производные по законам комплексного анализа, получим систему необходимых условий в действительных функциях от четырех действительных переменных. Из первого условия
приравнивая действительные и мнимые части в равенстве, получим
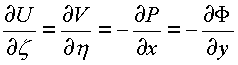 ,
, 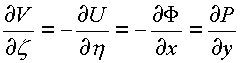
Из второго соотношения получим следующую систему равенств
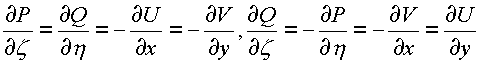
Таким образом, из комплексных соотношений получены необходимые условия независимости криволинейного интеграла от пути в пространстве в действительных выражениях. Покажем, что эти соотношения имеют место в пространстве. Координатное пространство от четырех независимых переменных будет иметь шесть проекционных площадок
![]() . К каждому
из интегралов применим формулу Грина и Стокса
получим:
. К каждому
из интегралов применим формулу Грина и Стокса
получим:
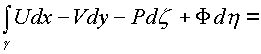
=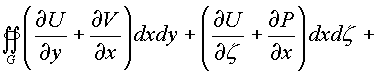
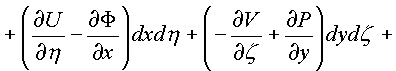
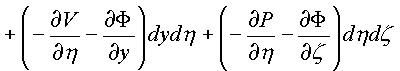
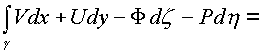
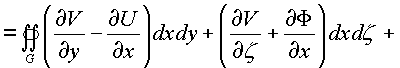
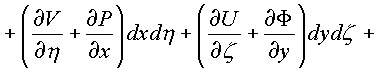
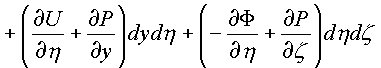
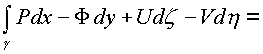
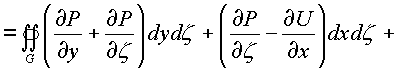
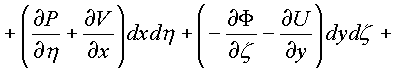
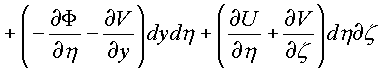
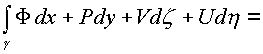
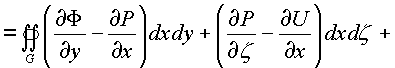
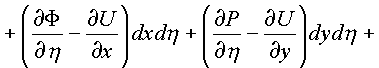
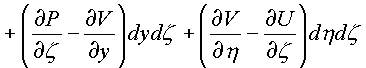
Независимость каждого криволинейного интеграла от пути в комплексном пространстве зависит от равенства нулю 24-х соотношений между частными производными, стоящими в подынтегральных скобках по каждой проекционной площадки поверхности Ф в пространстве.
Все 24-ре соотношения соответствуют равенствам, выведенным из условия независимости пространственного криволинейного интеграла, выраженного через комплексные независимые
Z,![]() . Подынтегральные соотношения
получены циклической перестановкой частных
производных по проекционным площадкам
дедуктивным распространением формул Стокса и
Грина в четырехмерное действительное
пространство. Таким образом, фактически
обоснована формула Грина и Стокса в
четырехмерном действительном пространстве.
. Подынтегральные соотношения
получены циклической перестановкой частных
производных по проекционным площадкам
дедуктивным распространением формул Стокса и
Грина в четырехмерное действительное
пространство. Таким образом, фактически
обоснована формула Грина и Стокса в
четырехмерном действительном пространстве.
Условия независимости криволинейного
интеграла в пространстве от пути С
интегрирования аналитической функции ![]() позволяют интеграл
позволяют интеграл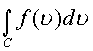 записать через интеграл
записать через интеграл
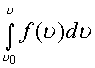 ,где
,где ![]() - концы кривой
С.В пространстве справедлива теорема о
первообразной функции для интеграла. Следуя
законам действительного и комплексного анализа Z, разберем теорему о первообразной
функции. Если функция
- концы кривой
С.В пространстве справедлива теорема о
первообразной функции для интеграла. Следуя
законам действительного и комплексного анализа Z, разберем теорему о первообразной
функции. Если функция
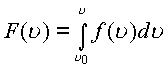 ,имеет
производную равную
,имеет
производную равную ![]() для всех точек области Д
пространства, то функция
для всех точек области Д
пространства, то функция ![]() будет первообразной функцией
будет первообразной функцией ![]() .Докажем, что
интеграл
.Докажем, что
интеграл
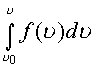 ,
, ![]() рассматриваемый от своего верхнего
предела, также является аналитической функцией в
Д пространства
рассматриваемый от своего верхнего
предела, также является аналитической функцией в
Д пространства ![]() , причем
, причем
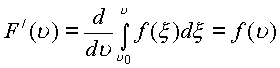
Определение производной в пространстве не изменено, поэтому для направлений с исключением изолированного, которое рассмотрим отдельно будем иметь
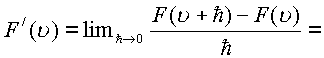
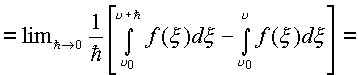
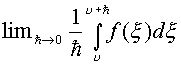
В силу непрерывности
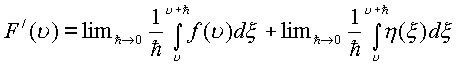
Первый предел равен
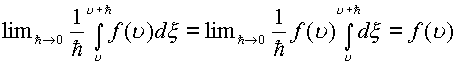
Если
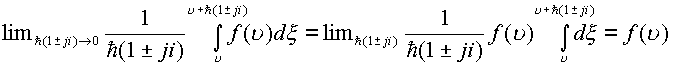
В первом случае
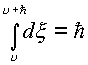 , во втором
случае
, во втором
случае 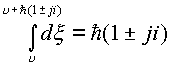
Второй предел запишем, используя свойство интеграла в виде
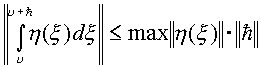
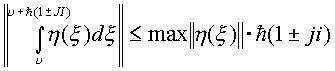 для
изолированного направления.
для
изолированного направления.
Таким образом ![]() , что и требовалось доказать. Все
классические функции анализа, имеющие табличные
производные, определены в пространстве и имеют
первообразную, так что
, что и требовалось доказать. Все
классические функции анализа, имеющие табличные
производные, определены в пространстве и имеют
первообразную, так что
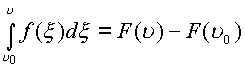
В пространстве ![]() справедливо следующее
утверждение: Интеграл от
аналитической функции
справедливо следующее
утверждение: Интеграл от
аналитической функции
![]() в
односвязной области G вдоль
любого замкнутого контура С, лежащего в G, равен нулю.
в
односвязной области G вдоль
любого замкнутого контура С, лежащего в G, равен нулю.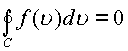 .
.
Основные свойства интегралов в действительной и комплексной области остаются в силе и в пространстве.
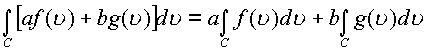 , где a, b
–любые действительные и
комплексные постоянные.
, где a, b
–любые действительные и
комплексные постоянные.
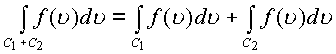 , где
, где ![]() -определяют кривую
-определяют кривую ![]()
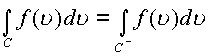 , где
, где ![]() кривая,
проходимая в противоположном направлении кривой
С. В силе остается еще одно свойство интеграла :
Пусть
кривая,
проходимая в противоположном направлении кривой
С. В силе остается еще одно свойство интеграла :
Пусть ![]() на кривой С и L длина С, и
на кривой С и L длина С, и ![]() длина кривой по
изолированному направлению, тогда
длина кривой по
изолированному направлению, тогда
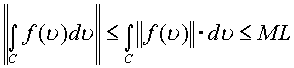 ,или
,или ![]() .
.
Это свойство вытекает из определения интеграла
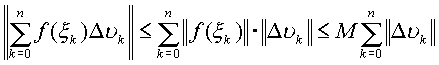 , где
, где 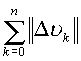 есть длина ломаной
есть длина ломаной ![]() , вписанной в
кривую С, так что в пределе при
, вписанной в
кривую С, так что в пределе при ![]() получаем L, а по изолированному направлению
получаем L, а по изолированному направлению ![]() .
Откуда и вытекает свойство.
.
Откуда и вытекает свойство.
Пример .
Вычислить криволинейный интеграл по кривой С от точки
Ввиду того, что функция
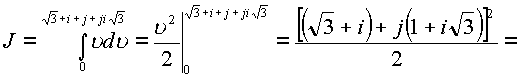
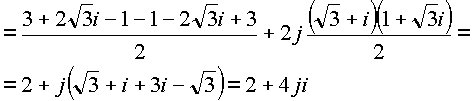
Рассмотрим решение в пространственных комплексных координатах
![]() может быть представлена двумя
точками пространственной комплексной плоскости
может быть представлена двумя
точками пространственной комплексной плоскости
![]() .Интеграл
распадается на два криволинейных интеграла
.Интеграл
распадается на два криволинейных интеграла
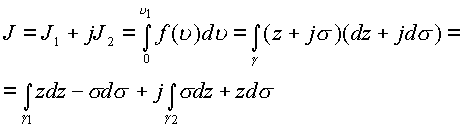
Рассмотрим для примера путь
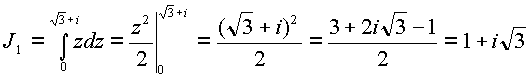
Интеграл
На линии
z—имеем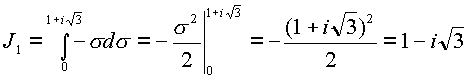
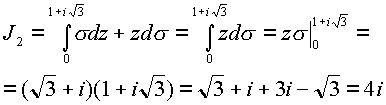
Следовательно по пути
Окончательно получим
![]()
Таким образом, получен предыдущий результат. Криволинейный интеграл не зависит от пути интегрирования.
Вычислим тот же интеграл в цилиндрических пространственных координатах
![]()
В этих координатах
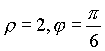
![]() , следовательно
, следовательно 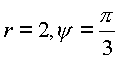
Согласно вышеизложенной теории интеграл также распадется на два интеграла
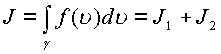 ,
где
,
где
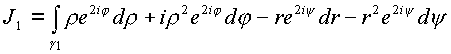
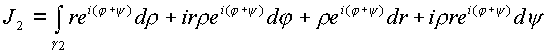
Интегрирование произведем по сумме простейших кривых в пространстве, чтобы на каждой из них изменялся один параметр из четырех рис
Интеграл по прямой 0—1 вычисляется при следующих параметрах
![]() , на линии
1—2 имеем
, на линии
1—2 имеем 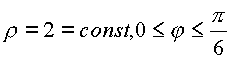
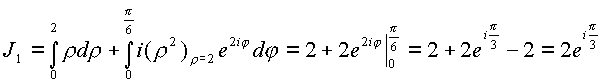
![]()
Рассмотрим путь 1—3, на котором
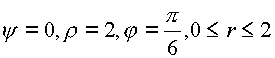
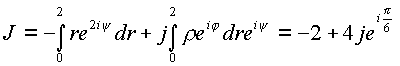
На линии 3
—5 меняется угол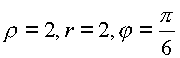 . Угол
. Угол 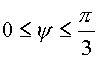 . Тогда
. Тогда
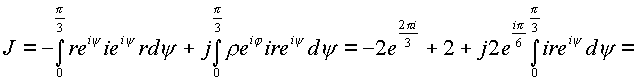
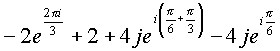
Произведем суммирование полученных результатов
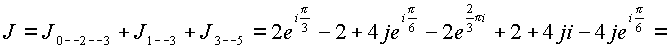
![]()
Результат соответствует ранее вычисленному. В цилиндрических координатах когда комплексы, составляющие элемент пространства имеют разные углы
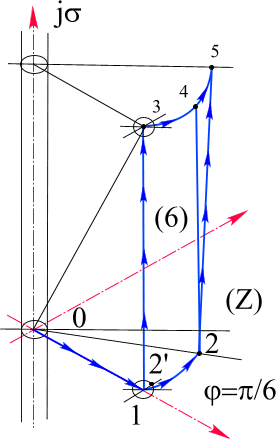
Рис. 24. Независимость криволинейного интеграла от пути в пространстве.
![]() . Комплекс,
стоящий в скобках
. Комплекс,
стоящий в скобках ![]() ,состоит из отрезка
,состоит из отрезка ![]() ,идущего
по действительной оси и криволинейного отрезка,
находящегося на цилиндрической аппликате
радиуса
,идущего
по действительной оси и криволинейного отрезка,
находящегося на цилиндрической аппликате
радиуса ![]() и имеющего начало в
и имеющего начало в ![]() точке
точке ![]() ,которая имеет угол равный
нулю, и точки
,которая имеет угол равный
нулю, и точки ![]() ,которая находится на высоте
,которая находится на высоте ![]() и закручена по
этой цилиндрической аппликате на угол
и закручена по
этой цилиндрической аппликате на угол![]() . Этот комплекс
повернут как одно целое на угол
. Этот комплекс
повернут как одно целое на угол![]() .
.
Каждая точка
z на плоскости Z в пространствеВычисление криволинейного интеграла в пространстве следует проводить в два этапа
:- в плоскости Z, приняв
- в плоскости
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com