 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
10.7. Особые области в комплексном пространстве
В комплексном пространстве
реализуются основные теоремы Коши о связи особой точки области с ее границей. Теоремы приобретают новые свойства и физическую интерпретацию. В комплексном пространстве под особой точкой понимается подпространство, которое принадлежит пространству более высокой размерности. Иными словами пространство более высокой размерности выступает по отношению к пространству более низкой размерности как особая точка ( или область).
Теорема 2. Пусть функция
дифференцируема в односвязной области G пространства 
и пусть простая замкнутая кривая 
лежит в G и ориентирована в положительном направлении.рис1
Тогда для любой точки
, лежащей внутри области, охватываемой поверхностью, натянутой на кривую 
, справедлива формула
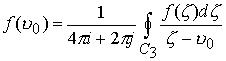
Теорема 3. Пусть функция
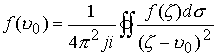дифференцируема в односвязной области G пространства и пусть имеется гладкая поверхность
, натянутая на простейшую пространственную кривую 
без точек самопересечения. Тогда для любой точки 
, лежащей внутри объема G, заключенного внутри замкнутой ( геометрически) поверхности, имеет место формула рис 3
, 
-дифференциал упомянутой поверхности
С точки зрения физики, при описании явлений взаимодействия, происходящих при формировании материи (материалов в более узком смысле), теорема говорит, что все внешние проявления разнообразных взаимодействий, таких как ядерные реакции, процессы взаимодействия оболочек атомов с квантами энергии и между собой (химические реакции), взаимодействие компонентов в сплавах, электрические, магнитные и электромагнитные взаимодействия, определяются именно внутренними особыми точками в области.
Поставим в соответствие математической области элементарную частицу как особую точку и предположим, что так же как многосвязные области взаимодействуют между собой через особые точки, так и элементарные частицы в каком-либо структурном образовании взаимодействуют посредством процессов, протекающих в особых точках.
В одномерном пространстве особой сингулярной точкой для функции 
является точка 
. В плоскости массивов (x,y) с интервалом 
особой точкой будет точка массива (0,0), в комплексной плоскости модуль точки совпадает с интервалом массивов, поэтому особой точкой является
окрестность нуля.
В трехмерном пространстве массивов (x,y,z) особой точкой является массив (0,0,0).
В комплексном пространстве особенность превращается в изолированную ось, которая соответствует подпространству делителей нуля.
Подпространство делителей нуля можно выразить в виде комплекса
В результате имеем комплекс не равный нулю, но имеющий модуль равный корню из нуля не равный автоматически нулю, вследствие наличия в структуре числа изолированного направления аргумента
В одномерном пространстве и двумерном как пространстве массивов так и комплексном пространстве корень из нуля равен нулю. В пространстве большего числа измерений для массивов в силу гипотезы Римана корень из нуля равен нулю.
В комплексном пространстве положение меняется, так как появляются изолированные направления. Фундаментальное свойства заряда быть положительным и отрицательным связано с наличием изолированного направления- особой точки в виде изолированной оси. Классификация заряда на лептонный, барионный, мезонный, гравитационный и так далее связано с размерностью пространства и количеством изолированных направлений, определяемыми разными комбинациями мнимых единиц –
чисел. В самом общем выражении пространство одного измерения является зарядом по отношению пространства другого по размерности измерения. Гравитационный заряд одного знака, так как соответствует предельному по размерности пространству.П. Дирак при открытии магнитного монополя давал физическую интерпретацию интегралов относительно особой точки в таком же разрезе.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com