3.4.3. Изолированное направление

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

В связи с этим необходимо исследовать вопрос о изолированном направлении в пространстве и соотношении введенного параметра со скоростью и скоростью То, что пространство-время обладает особенностью в виде изолированной оси видно из записи интервала который можно представить в виде

Если интервал равен нулю, то

и формула интервала превращается в произведение делителей нуля

. Поэтому, если имеются две системы отсчета, допустим штриховая и не штриховая, то при равенстве временных и пространственных координат системы выстраиваются по изолированному направлению, где соблюдается равенство

В этом случае квадрат модуля равен нулю, однако комплекс

(3.4.26.)

Временная координата в изолированном направлении равна по величине пространственной координате. Начало координат имеет окрестность нуля. Начало временной координаты повернуто относительно пространственной на угол Наличие этой особенности не учитывается в теории относительности.

Теория относительности использует вариант действительного аргумента в виде (3.4.20.) и (3.4.21.). В этих выражениях произошла потеря решения, связанная с наличием особенности

в пространстве. Поэтому рассмотрим аргументы в виде

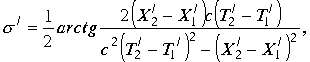
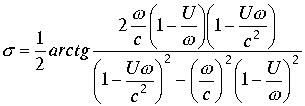
Рассмотрим выше разобранные условия: при 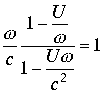,, в этом случае имеем проекцию на временную ось координат. При Вновь получена проекция на временную ось координат. Предыдущий расчет давал в этом случае проекцию на пространственную ось. Поэтому рассматривается изолированное направление, когда в комплексных координатах, или , когда аргумент взят в действительных числах. В первом случае имеем из выражения (3.4.16.) , во втором случае знаменатель дроби функции 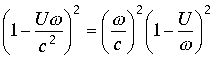должен быть равен нулю . Последние выражения эквивалентны друг другу, поэтому в пространстве изолированное направление выражаемое функцией арктангенс в изолированной точке 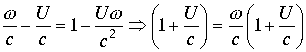равноценно по условию, когда функция арктангенс равна бесконечности. Проведем преобразования дроби .Откуда имеем 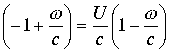при любом . Преобразования можно провести в другой последовательности и получить . 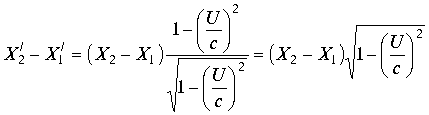Откуда следует, что при любомимеем выполнение условий когда. Аргумент при выполнении двух условий дает проекцию комплекса на изолированную пространственную ось. В этом случае временная координата равна нулю. Таким образом, условие теории относительности , при котором координатаравносильно условиям Условие , при котором имеем проекцию комплекса на временную ось, когда , равносильно условию Системы отсчета движутся относительно друг друга вдоль направления пространственной оси со скоростью .Только при этих условиях соблюдается правильность математических операций. Если условие подставить в координату (3.4.7.), то получим

В координатном представлении (3.4.7.) и (3.4.8.) оси имеют единственную скорость и скоростной параметр , поэтому условия теории относительности связаны между собой и определяют проекции координатных осей, подменяя обычные тригонометрические функции . В соответствии с формулой (3.4.26.), интервал теории относительности при движении со скоростью света одной системы отсчета относительно другой системы по оси , определяется равенством

Если системы отсчета движутся относительно друг друга со скоростью света С, то интервалы по осям координат равны:

В этом случае события имеют мнимую точку как в системе отсчета штриховой так и не штриховой при координатной записи интервала. Если координаты систем отсчета записываются в сферических координатах, то каждая система находится в световом -туннеле, который мы называем изолированным направлением, вследствии равенства аргументов . Интервал в этом случае превращается в сферу радиуса . Координатная ось jix становится -туннелем, имеющим радиус , рис 40 размеры которого расчитываются из энергетических соображений, см пункт 3.1 формулы (3.4.) и (3.5.)

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com