1.3.1. Связность комплексного пространства

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

Пространственные комплексные координаты, введенные в исследование, по-новому определили точку в пространстве связность, непрерывность этого пространства.

Комплексная ось является естественным продолжением в построении системы комплексных координат, ибо к плоскости (z) восстановлена плоскость, только свернутая в цилиндрическую поверхность с радиусом корня из нуля. При построении комплексной плоскости (z) оси x и y топологически равноценны и выступают как обозначения, которые можно переставить. Продолжая этот принцип к плоскости (z), была восстановлена также плоскость (s ), свернутая в цилиндр, на поверхности которого остаются в силе все метрические соотношения, заданные на плоскости: сумма углов треугольника по прежнему равна 180 град., равными остаются расстояния между вершинами и величина площади. Гауссова кривизна цилиндра равна нулю. В этом смысле декартова система координат становится совершенно непригодной из-за того, что третья ось не несет топологии плоскости, к которой она восстановлена.

На внешней поверхности выколотой оси js можно получить все точки плоскости (z). В цилиндрических координатах, каждая точка n имеет окрестность g _r, с радиусом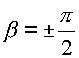 , которая расположена от плоскости (z) на расстоянии r. (см. рис. 4, 5, 6, 7). Поверхность выколотой оси js содержит точки, у которых угол . Тогда согласно формуле (1.5.) можно записать

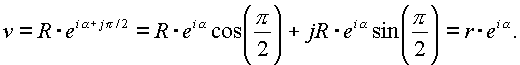
Поэтому изолированное направление ± j arctg(i) следует считать заключенным внутри этой выколотой оси, а бесконечное множество делителей нуля n _д образует внутреннюю поверхность выколотой оси. Все это бесконечное множество, расположенное на конусе с мнимой поверхностью в цилиндрической системе координат, собирается в выколотую ось в сферических координатах. Мнимый конус-фильтр состоит из окрестностей точек g _r, поверхность которых повернута относительно поверхности обычных точек n на p /2 согласно условию (1.8.).

Точка делителей нуля в цилиндрических координатах имеет место (рис. 8), однако в нее нельзя провести радиус-вектор, поэтому поверхность, образованную множеством этих точек, считаем мнимой. Эта поверхность образована множеством не суммируемых, взаимно перпендикулярных векторов с равными по величине модулями и имеющих начало в равных точках окрестности нуля , повернутых одна относительно другой на угол p /2.

Из классического анализа известно, что для получения взаимно однозначного отображения необходимо из пространства координат исключить некоторую область: в простейшем случае это нуль, в сферических координатах это линия, в комплексной z - плоскости это окрестность нуля.

Согласно формуле (1.5.) сферические комплексные координаты выражаются в виде:

Якобиан отображения пространства n в пространство n (R, f , y ) будет равен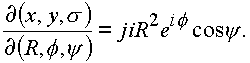

Формула показывает, что якобиан равен нулю в следующих случаях:

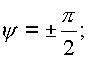
Первый случай тривиален, второй рассмотрен выше и указывает на исключение из рассмотрения поверхности выколотой оси. Третий случай говорит о том, что если из пространства (n ) выбросить выколотую ось радиуса , то вследствие наличия в якобиане квадрата радиуса на пространства одновременно выбрасывается все множество делителей нуля n _д, которые характеризуются углами y , равными изолированному направлению arctg i.

Исключение из пространства выколотой оси равносильно исключению нуля в z-плоскости. Наличие в пространстве (n ) выколотой оси ставит по-новому вопрос о связности пространства кривых и поверхностей в нем.

Для реализации интегральных теорем Коши необходимо рассмотреть вопрос об односвязности поверхности, которая натягивается на циклическую пространственную кривую. В комплексном пространстве решающее значение имеет характер кривой и ее расположение относительно выколотой оси. Реализация естественно зависит и от подынтегральной функции.

В классическом анализе связность пространства определяется теоремами Стокса и Остроградского. В z-плоскости реализована только теорема Стокса. Для применения теоремы Стокса требуется, чтобы Контур и поверхность, которая натянута на этот контур, целиком лежали в области, где выполнены соответствующие условия. Теорема Остроградского остается в силе и для объема с порами (рис. 15). Под термином "пора" понимается ограниченная область, целиком лежащая в рассматриваемой области и исключенная из рассмотрения.

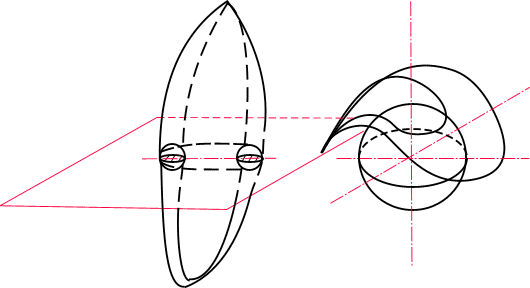
Рис. 15. Поры в пространстве.

На рис. 16, 17 даны примеры из классического анализа односвязного и многосвязного.

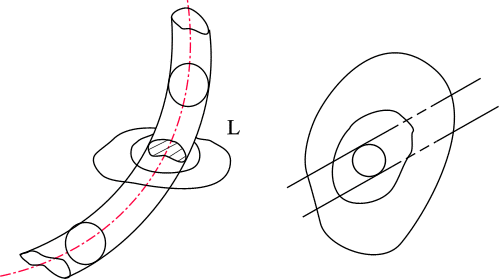
pic16.gif (9968 bytes) Рис. 16. Кривая a, не стягиваемая в точку

Рис. 16. Кривая a, не стягиваемая в точку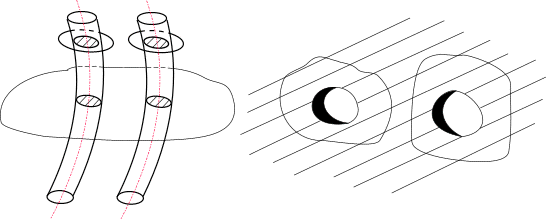

Рис. 17. Пример многосвязного пространства

В связном пространстве контур стягивается в точку непрерывным образом, причем и сама точка принадлежит рассматриваемой области. В односвязном, двухсвязном и многосвязных пространствах контур z не может быть стянут в точку непрерывным образом, как это показано на рис. 16, 17, не пересекая при этом границы области. Это примеры общего логического плана.

В комплексном пространстве выколотая ось, стянутая из точек мнимой поверхности конуса выступает как бесконечная трубка радиуса , заключающая в себе пространство другого измерения, а ее поверхность является границей раздела пространств разной по величине размерности (рис. 18). Трубка приходит из бесконечности и уходит в бесконечность.

Кривые С₀, С₁, С₂ (рис. 19), охватывающие выколотую ось, нельзя стянуть в точку радиуса ноль, так как ноль в пространстве имеет окрестность радиуса корня из нуля.

Кривую С₀ можно стянуть в точку, так как она охватывает выколотую ось (рис. 19).

Кривая С₁, лежит в плоскости, параллельной плоскости (z), и стягивается в окружность радиуса .

Кривая С₃ является простейшей пространственной кривой, на которую можно натянуть непрерывным образом без точек самопересечения поверхность так, чтобы внутри содержался объем.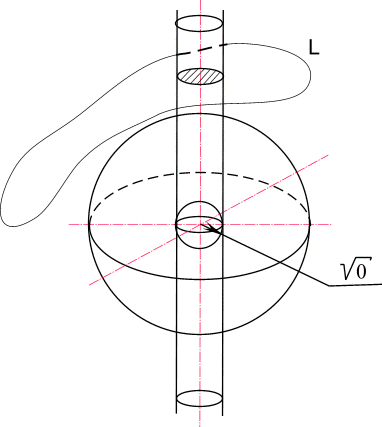

Рис. 18. Изолированная ось в комплексном пространстве, обуславливающая его связность.

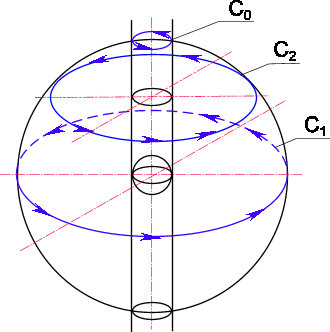
Рис. 19. Кривые C₀, C₁, C₂, стянутые в точку из-за наличия в комплексном пространстве изолированного направления.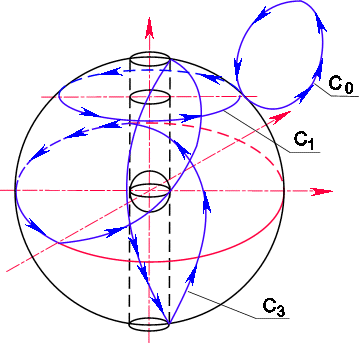

Рис. 20. Кривая C₀, стянутая в точку, кривая С₁, не стянутая в точку, и кривая С₃ - простейшая циклическая кривая в пространстве.

Простейшей комплексной кривой в z-плоскости является окружность. Натянуть на окружность поверхность так, чтобы в ней был заключен объем, не представляется возможным.

Контур С₃ является простейшим пространственным контуром, он состоит из кривой, идущей по внешней поверхности сферы, и кривой, идущей по внешней поверхности выколотой оси.

Пространство (n ) может быть сжато в комплексную плоскость с выколотыми осями по z, js Замкнутая кривая C₄ будет обходить выколотые оси по полуокружностям.

Кривая C состоит из двух окружностей, лежащих во взаимно перпендикулярных плоскостях (см. рис. 21).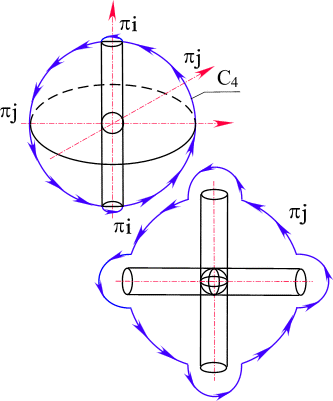

Рис. 21. Пространственная кривая C₄, охватывающая две изолированные оси. Внутренний контур кривой C₃ можно деформировать так, что он пойдет по внутренней поверхности сферы, при этом образуется оболочка толщиной d (рис. 17).

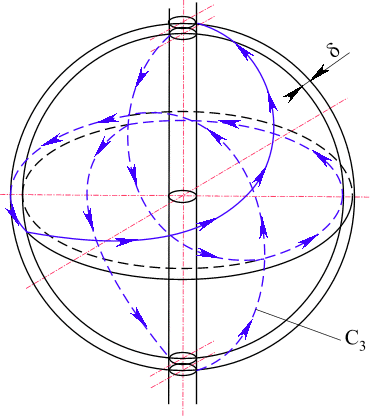
Рис. 22. Деформация простейшей пространственной кривой C₃ с выделением поверхностного слоя d .

Оболочку можно увеличить до толщины S, как это показано на рис. 23. В этом случае пространство будет заключено между двумя сферическими поверхностями, соединенными между собой цилиндрической поверхностью выколотой оси. Иными словами, в любом случае простейшей поверхностью становится тороидальная поверхность.

Дадим определение кривой C₃ в пространстве (n ), которую назовем главной простой кривой в пространстве.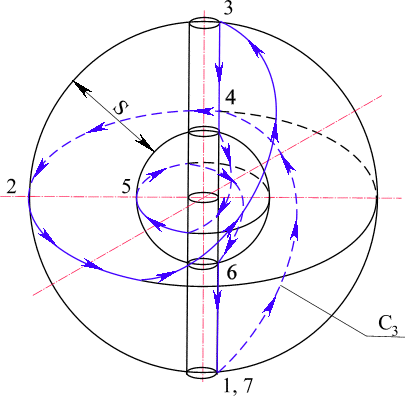

Рис. 23. Деформация простейшей пространственной кривой С₃ с выделением шарового слоя S.

Определение. Простой кривой в пространстве трех (четырех измерений будем называть кривую С₃ (рис. 20) которая получается деформацией из плоской кривой длины 2p R₀, путем натягивания ее на сферу с выколотым e -туннелем, так, что часть кривой, равная 2Re , проходит через e -туннель, а остальная часть, равная 2p R₀-2Re , проходит по поверхности сферы так, что сфера при фиксированном R₀ имеет наибольший радиус. При этом точка n , проходящая один раз замкнутую кривую C₃, делает в e -туннеле и по поверхности сферы в исчислении по углу f два полных оборота 4p , а по углу y один оборот 2p .

Если двигаться по кривой C₀ (рис. 20), то из точки вернемся в ту же точку без изменения аргументов.

Кривые C₀, C₁, C₂ (рис. 19) лежат в плоскости, параллельной z-плоскости, поэтому для них y =const и при обходе изменяется только аргумент f , добавляя к своему значению за один оборот. 2p .

Движение по кривой C₃ (рис. 20) дает приращение аргументов , . В общем случае, кривая С_i может иметь различные исчисления по аргументам f , y в зависимости от того, как она проходит выколотую ось.

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com