Продолжение 3 из 3. 1.7.3. Вычисление определенных двойных интегралов с помощью вычетов.

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

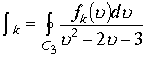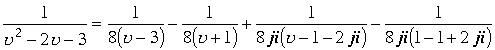Вычислим ряд криволинейных интегралов. , где функцию возьмем последовательно равной . Раскладывая дробь на сумму простейших дробей относительно полюсов дроби в пространстве , будем иметь

где сумма после двух дробей учитывает полюса дроби , при равенстве знаменателя нулю в изолированном направлении . Корни знаменателя дроби 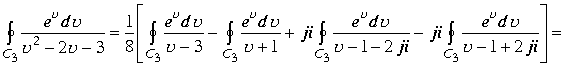,являются полюсами функции подынтегрального выражения при условии если кривая натянута на поверхность , которая заключает в себе область со всеми точками, определяемыми в пространстве этими корнями. Функции регулярны в этих точках. Составим интеграл для первой функции , к интегралам можно применить формулу Коши

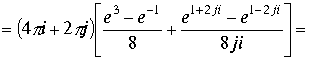
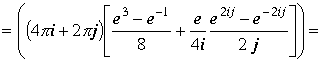
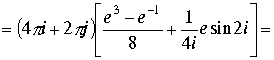
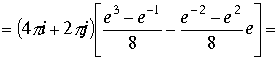
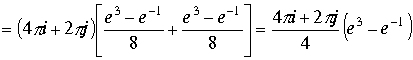Вычисляем следующий интеграл для функции

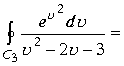
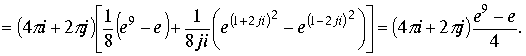
Для функции 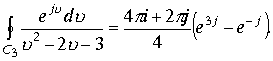имеем . Для функции .

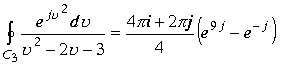Разложение подынтегральной функции на четыре дроби, две из которых представляют разложение по изолированному направлению в пространстве и дальнейшее вычисление интеграла показывают , что сумма первых двух интегралов от разложения равна сумме интегралов по изолированному направлению. Это в том случае, если область интегрирования , охватываемая пространственной кривой , содержит все пространственные полюса. Если область G заключена между поверхностями ,натянутыми на эквидестантные кривые , то для полюсов функции справедлива формула .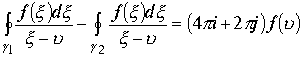

Применим эту формулу к расчету первого интеграла для различных областей . Предположим, что кривая натянута на поверхность сферы радиуса а кривая на поверхность сферы радиуса . В этом случае область G содержит две точки ,которые являются полюсами подынтегральной функции. Интеграл по кривой распадается на разность двух интегралов по кривой и кривой . Кривые подобны кривой

, Используя разложение подынтегральной функции на дроби в пространстве , получим выражение для суммы вычетов функции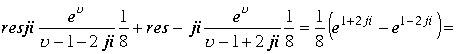

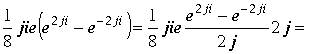
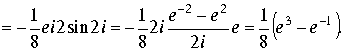
Подставляя в интеграл, получим .

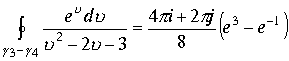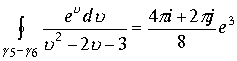Если область G заключена между поверхностями , натянутыми на кривые , со сферическими радиусами соответственно , то подынтегральная функция будет иметь один полюс .Интеграл будет равен .

Произведем выделение первых мнимых и действительных частей в правой и левой части вычисленного интеграла. Предварительно проведем операции и введем обозначения для сокращения записи формул. ,где .

где

В этих обозначениях проведем выделение мнимой и действительной частей подынтегральной функции

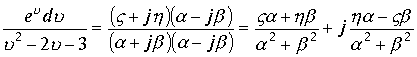. Подставим в исходный интеграл и приравняем правые и левые действительные и мнимые части

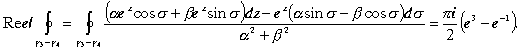
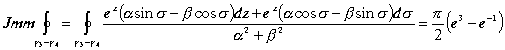Определим проекцию интеграла по кривым на плоскость Z . В этом случае надо принять

. Проекция пространственного интеграла на плоскость Z равна

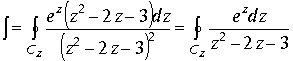. При отображении область между двумя концентрическими сферами перейдет в область между двумя окружностями. Область будет содержать полюса функции в плоскости Z .Интеграл можно вычислить по формуле Коши.

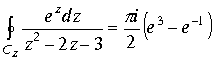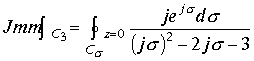Рассмотрим проекцию интеграла на изолированную ось ,которая также представляет комплексное плоское пространство. Проекция одновременно является мнимой частью пространственного интеграла

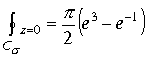Комплексная ось имеет две изолированные точки . Если точки входят в область определения интеграла, то по интегральной формуле Коши его можно вычислить

. Мнимая часть от пространственного интеграла также равна этой величине. Результаты совпадают. Рассмотрим результаты вычислений проекций на комплексные плоскости Z,, через пространственный интеграл, и сравним их с вычислениями этих проекций в плоскостях для различных областей определения пространственного интеграла.

Область охватывает только одну изолированную точку . В этом случае

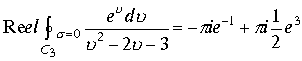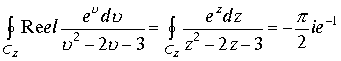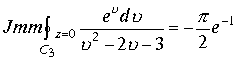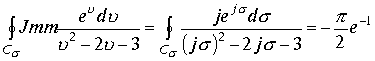Если область определения интеграла включает в себя три изолированные точки , то имеем

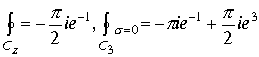
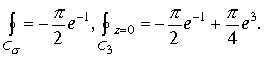
Если область определения пространственного интеграла содержит все изолированные точки

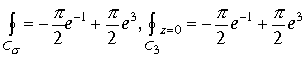
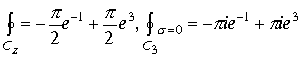
В пункте 1.7.2 рассмотрена связь изолированных точек в пространстве на примере рис 32 и рис33. Изолированные точки проектируются особым образом в точки .Поверхность сферы , изолирующая особую точку в пространстве , разделяется на нижнюю и верхнюю полусферу . Соответственно этому ведут себя и пространственные кривые , окружающие эти точки. При проектировании на плоскость Z эти полусферы в зависимости от их расположения переходят в нижнюю или верхнюю полусферу точек , лежащих в этой плоскости. Этим объясняется расхождение результатов интегрирования в пространстве от вычислений интегралов от проекций подынтегральной функции на плоскости Z или .Решение квадратного уравнения в плоском пространстве не содержит пространственных корней , определяемых на основе существования делителей нуля. В то же время изоляция полюса окружностью малого радиуса в плоскости есть след третьей изолированной оси на плоскости .

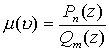Если функция представлена как частное от деления двух многочленов степени n и m,

, то для сходимости интеграла в плоскости Z необходимо, чтобы степень многочлена в знаменателе функции превышала степень многочлена числителя на две единицы

и функция может в пределе рассматриваться в виде

,, , где к-целое. В этом случае модуль при достаточно больших R.

Тогда имеем

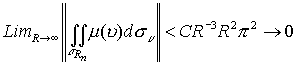
Тем самым выявлено условие сходимости интеграла и доказана лемма

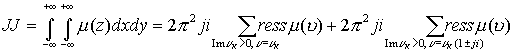
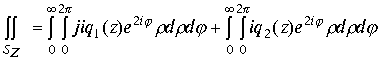где .

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com