 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
7.4. Комплексное пространство тяготения.
Рассмотрим следующий пространственный комплекс
Преобразуем комплекс
, где обозначено 
, 
, 
.
Таким образом, пространственный комплекс
имеет модуль 
и соответствует форме интервалу Минковского.
Комплексное пространство имеет две цилиндрические оси
и третью сферическую ось 
. При равенстве 
из пространства выделяется изолированное направление 
. В пространстве выделяется пространство делителей нуля, которое в физических исследованиях несет функцию полевой материи
.
Корень из нуля определяет окрестность нуля в начале координат и определяется из физических условий.
Для метрики Шварцшильда имеем:
,
, 
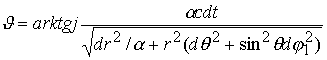
При этих обозначениях, комплекс в пространственных сферических координатах представим в виде
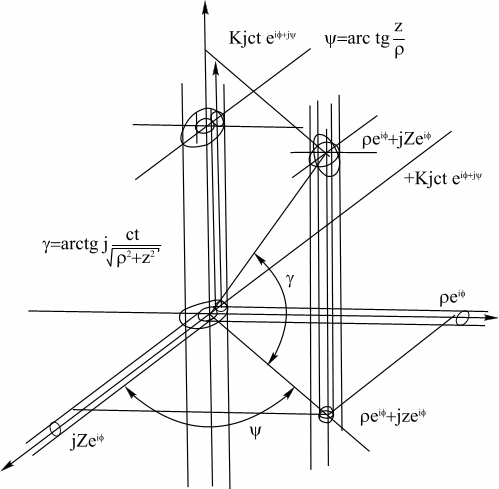
Рис.64. Модуль комплексного пространства равен интервалу Минковского.
В этом комплексе два угла действительны 
, один угол комплексный 
, который в конечном счете и определяет четырехмерное псевдоевклидовое пространство. Метрика 
в этом пространстве является интервалом поля тяготения Шварцшильда. Исследуем этот комплекс. Введем условия для определения изолированного направления и 
-окрестности начала координат. Для этого необходимо выполнения равенства 
. По законам алгебры пространственных комплексов это условие равносильно равенству нулю модуля комплекса, которым в данном случае равен квадрату интервала
.
, где
, при условии 
множитель, стоящий в скобках должен быть равен нулю, поэтому пространственный комплекс записывается в виде
Из условия для определения изолированного направления и равенства нулю интервала поля Шварцшильда получили разложение комплекса на две равных по величине составляющих, которые развернуты относительно друг друга на 90 град. и приложены к разным точкам окрестности начала координат. Физически это разложение отвечает полевой структуре той гравитационной массе, которая заключена в окрестности координат. Эта масса определяет кривизну пространства. Величина
представляет корень квадратный из метрического тензора 
риманова пространства –времени. 
.
Равенство нулю интервала Шварцшильда определяет наличие в начале координат тяжелой массы М, которая сосредоточена в изолированном пространстве гравитационного радиуса
. Гравитационный радиус определяется по формуле 
, поэтому имеем 
. Гравитационная масса М по структуре содержит в себе изолированное направление 
, которое можно рассматривать как цилиндрическую ось гравитационного радиуса в сечении равного 
. В тоже время можно рассматривать гравитационную массу М сосредоточенную в сферической окрестности начала координат как гравитационный заряд, принадлежащий пространству более высокой размерности. Если отношение
то составляющие гравитационного поля переходят в пространство более сильного заряда. Равенство 
определяет размерность пространства для конкретной массы М. Тривиальное соотношение между массами и их гравитационными радиусами 
разделяет один
гравитационный радиус от другого.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com