1.3.4. Интегральная формула Коши.

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

Выведем аналог интегральной теоремы Коши в пространстве .

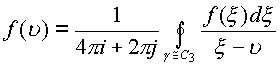
Теорема. Пусть функция дифференцируема в односвязной области G пространства и пусть кривая замкнута, лежит в G и ориентирована против часовой стрелки. Тогда для любой точки , лежащей внутри поверхности S, натянутой без точек самопересечения на кривую , справедлива формула

Доказательство. Функция 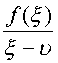дифференцируема по в области G с выколотой точкой .

Область G в пространстве это область ограниченная поверхностью S, натянутой на кривую

без точек самопересечения. В любом пространстве кривая должна проходить через туннель, так как в противном случае она при стягивании в сферу выродится в точку не содержащую область G пространства. Через точку проведем туннель и окружим ее кривой типа кривой, так чтобы она целиком лежала в области G вместе с поверхностью , натянутой на эту кривую. В этом случае изолированная ось будет проходить через точку и сферу, радиус которой .То есть зададим и границу .Тогда согласно интегральным теоремам будем иметь

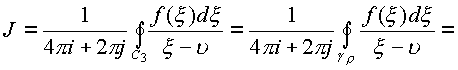
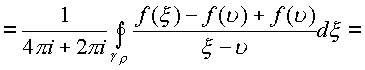
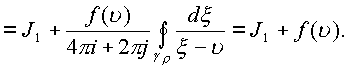Где остается доказать, что

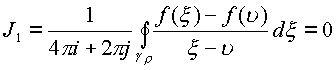. Для доказательства воспользуемся оценкой модуля этого интеграла.

Функция непрерывна в точке , поэтому найдется соотношение , при ,где , а , в том числе и по изолированному направлению , при,где , а

.Следовательно

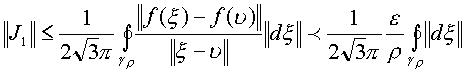Интеграл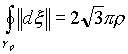, а для изолированного направления 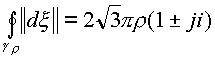, но

В этом случае . Вследствие этого во всех возможных вариантах интеграл имеет одну оценку .Поэтому при стремлении и в том случае когда , как коэффициент при делителях нуля, интеграл равен нулю. Формула доказана.

Если область G заключена между двумя поверхностями , натянутыми на эквидистантные

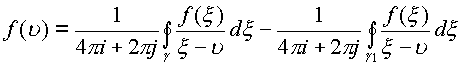
Пространственные кривые , то для точек этой области справедлива формула

Интегрирование по кривым идет в противоположных направлениях.

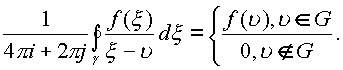
Если точка лежит вне замкнутой поверхности S, то подынтегральная функция аналитична всюду и интеграл равен нулю. Итак

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com